Section 4.4: Are There Congruence Shortcuts?
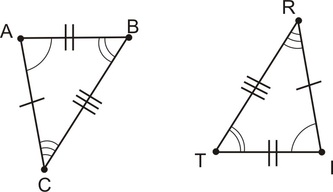
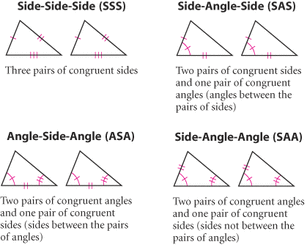
When two triangles are congruent, all three pairs of corresponding sides are congruent and all three pairs ofcorresponding angles are congruent. If all three pairs of corresponding sides are congruent, the triangles are congruent. This congruence shortcut is known as side-side-side (SSS). Another shortcut is side-angle-side (SAS), where two pairs of sides and the angle between them are known to be congruent. SSS and SAS are important shortcuts to know when solving proofs.
If two triangles are congruent, all three corresponding sides are congruent and all three corresponding angles are congruent. If two pairs of corresponding angles and the side between them are known to be congruent, the triangles are congruent. This shortcut is known as angle-side-angle (ASA). Another shortcut is angle-angle-side (AAS), where two pairs of angles and the non-included side are known to be congruent. ASA and AAS are important when solving proofs.
In right triangles, if two legs are congruent and if the two hypotenuses are congruent, then the triangles are congruent. This is known as the hypotenuse leg theorem. Note that this is the SSA shortcut which does not apply to non-right triangles. Applying the Pythagorean Theorem shows that only one value is possible for the other leg. Therefore, the two triangles are also congruent by the SAS or SSS congruence shortcut.
If two triangles are congruent, all three corresponding sides are congruent and all three corresponding angles are congruent. If two pairs of corresponding angles and the side between them are known to be congruent, the triangles are congruent. This shortcut is known as angle-side-angle (ASA). Another shortcut is angle-angle-side (AAS), where two pairs of angles and the non-included side are known to be congruent. ASA and AAS are important when solving proofs.
In right triangles, if two legs are congruent and if the two hypotenuses are congruent, then the triangles are congruent. This is known as the hypotenuse leg theorem. Note that this is the SSA shortcut which does not apply to non-right triangles. Applying the Pythagorean Theorem shows that only one value is possible for the other leg. Therefore, the two triangles are also congruent by the SAS or SSS congruence shortcut.
Notes and Powerpoints
| lessons_4.4_and_4.pdf | |
| File Size: | 32 kb |
| File Type: | |
| three_pairs1.gsp | |
| File Size: | 241 kb |
| File Type: | gsp |